العدد هو عنصر في سَتَلَة (متتالية) وحيدة من العناصر تُستعمل في عدّ تجميع أفراد. والأرقام العشرة [0، 1، 2، 3، 4، 5، 6، 7، 8، 9] تكوّن اللبنات الأساسية التي يمكن انطلاقا منها تركيب مجموعات من الأعداد. يُسمّى العدّ الذي نستعمله بنظام «العدّ العشري الوضعي»، وهو نظام عالي الفعّالية، ويمكن من خلاله تمثيل كمّيات ولو كبيرة جدّا باستعمال عدد محدود من الأرقام. كان تعريف العدد قديما مرتبطا بالسياقات المختلفة، وقد فكّك علماء الإسلام الكثير من المسائل التياسية من خلال الهندسة، وفي سنة 1899م وضع الإيطالي يوسيبي بيانو Giuseppe Peano بناءً منطقيا يتمثّل في قائمة من خمس مسلّمات تؤسّس بطريقة تياسية مجرّدة عن كلّ سياق مفهوم العدد الذي كانت عناصره المتفرّقة معروفةً منذ ما قبل التاريخ. والمُسلّمة عبارة عن «مطلب ذهني»، بمعنى أنّها فكرة يجب التسليم بها من دون مناقشة من أجل التقدّم في الموضوع، وتقترح المسلمّة الأولى من مسلّمات بيانو الخمسة اعتماد وجود رقم طبيعي كاملٍ أوّل، هو الصفر. المسلّمة الثانية تُعلن أنّ ما من عدد طبيعي كامل إلاّ ويليه عدد طبيعي كامل آخر. بذلك أصبح للصفر عدد يليه، سيكون اسمه واحد (1) وسيتطلّب هو بدوره عددا آخر يليه، سيكون اسمه اثنان (2) وهكذا دواليك. أمّا المسلمّة الثالثة فمقتضاها أنّ الصفر ليس تالي لأي عدد، فلا عدد قبله، والمسلّمة الرابعة هي أنّ عددين طبيعيين مختلفين لا يمكن أن يكون تاليهما العدد نفسه، ممّا يمنع من أن يكون العدد 77 على سبيل المثال متبوعا بالعدد 15. أمّا المسلّمة الخامسة فهي ما يُعرف باسم أداة التواتر outil de récurrence التي تتيح للتياسيين أن يتناولوا مجموعة الأعداد الطبيعية بمجملها عِلمًا أنّها مُتلانِية أي غير منتهية كما تتيح تعريف عمليتي جمع وضرب الأعداد الطبيعية الكاملة.

الأعداد الحقيقية هي كلّ الأعداد العادية وغير العادية، وتلك التي لا نستطيع التعبير عنها بالكسور، مثل نصف محيط الدائرة التي قابها (نِصْفُ قطرها) الوحدة، والذي نعبّر عنه بقيم تقريبية: ط= ..3,14159265 وغيرها، وتمثّل الأعداد الحقيقية بنقط على خطّ أفقي، حيث يقابل كلّ عدد حقيقي نقطة واحدة فقط، والعكس صحيح كذلك، أي أنّ كلّ نقطة على الخطّ الأفقي يقابلها عدد حقيقي واحد فقط، ويُسمّى هذا الخطّ بخطّ الأعداد الحقيقية. إنّ مجموعة الأعداد الطبيعية مجموعة جزئية من مجموعة الأعداد الصحيحة، وهي بدورها مجموعة جزئية من الأعداد العادية، وهذه الأخيرة مجموعة جزئية من الأعداد الحقيقية، وتعتبر مجموعة الأعداد الحقيقية مجموعة مُتَلانية أي غير منتهية.

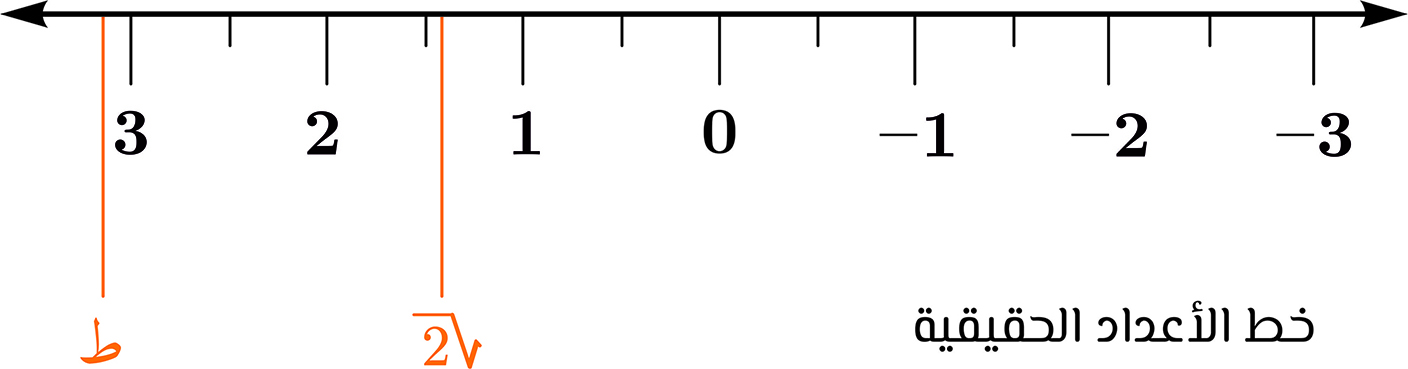
تبدأ قراءة الأعداد الصحيحة في العربية من اليمين سيرا إلى اليسار أي بدءا من الآحاد ثم العشرات ثمّ المئات ثمّ الآلاف ثمّ عشرات الآلاف ثمّ مئات الآلاف ثمّ الأبْلاف ثمّ عشرات الأبلاف ثمّ مئات الأبلاف ثمّ الأجْلاف ثمّ عشرات الأجلاف ثمّ مئات الأجلاف ثمّ الأدلاف وهلمّ جرجرة إلى الشّلْف وهو العدد الذي يرمز إليه بعشرة مرفوعة لقوّة موجبة قدرها 84. لأنّنا نقول على سبيل المثال تسعة وعشرون، وواحد وخمسون، فتسعة وواحد اللتان بدأنا بهما العدّ من الآحاد، بينما عشرون وخمسون من العشرات ثمّ لا بدّ أن تلي العشرات المئات على هذا السياق ثم الألوف ثم البُلوف، الخ. وهذا ما ذهب إليه مجمع اللغة العربية في القاهرة، حيث أجاز في قراءة الأعداد المركّبة أمرين: عطف الأقلّ على الأكثر، نحو: أحدٍ ومئة، وعطف الأكثر على الأقلّ، نحو: مئة وأحد، والأرجح عنده عطف الأقلّ على الأكثر، بالقراءة من اليمين إلى اليسار اتّباعا لما ورد في كتب النحو. أمّا الأعداد العشرية أو الكسيرة فتبدأ قراءتها من الفاصلة سيرا نحو اليمين، أي تبدأ من الأعشار ثمّ الأعشرة، ثمّ المعاشير أو المآليف ثمّ أعشار المآليف ثم أعشرة المآليف ثمّ المباليف ثمّ أعشار المباليف ثمّ أعشرة المباليف ثمّ المجاليف ثمّ أعشار المجاليف ثمّ أعشرة المجاليف، وعلى هذا النحو فيما بقي منها حتّى المشاليف، والمِشلاف هو العدد الذي يرمز إليه بعشرة مرفوعة إلى قوّة سالبة قدرها 84.

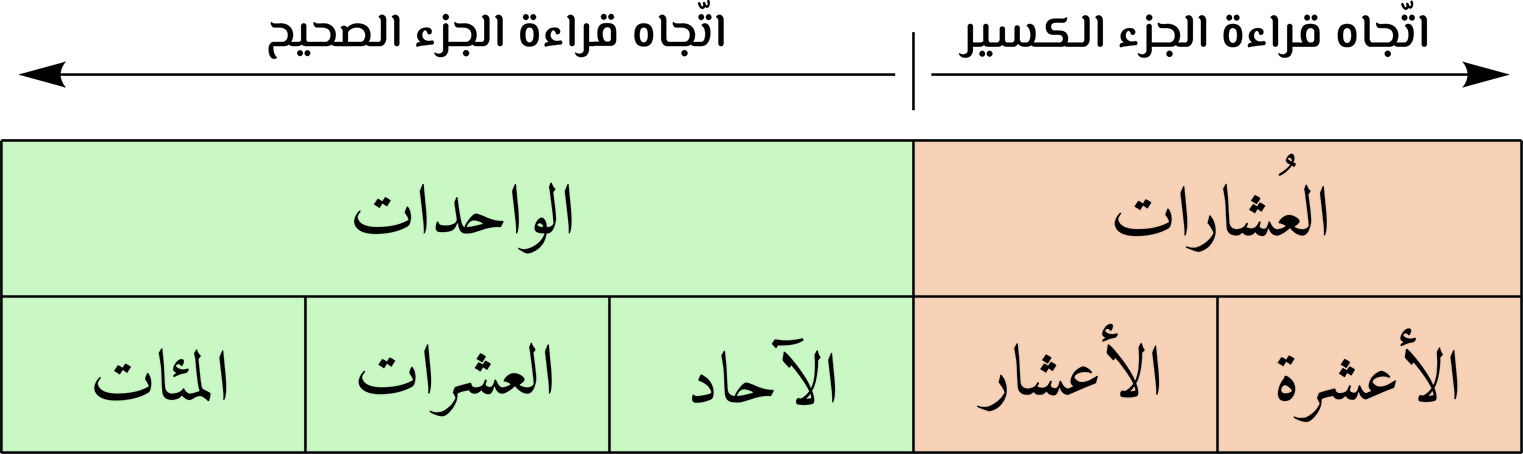
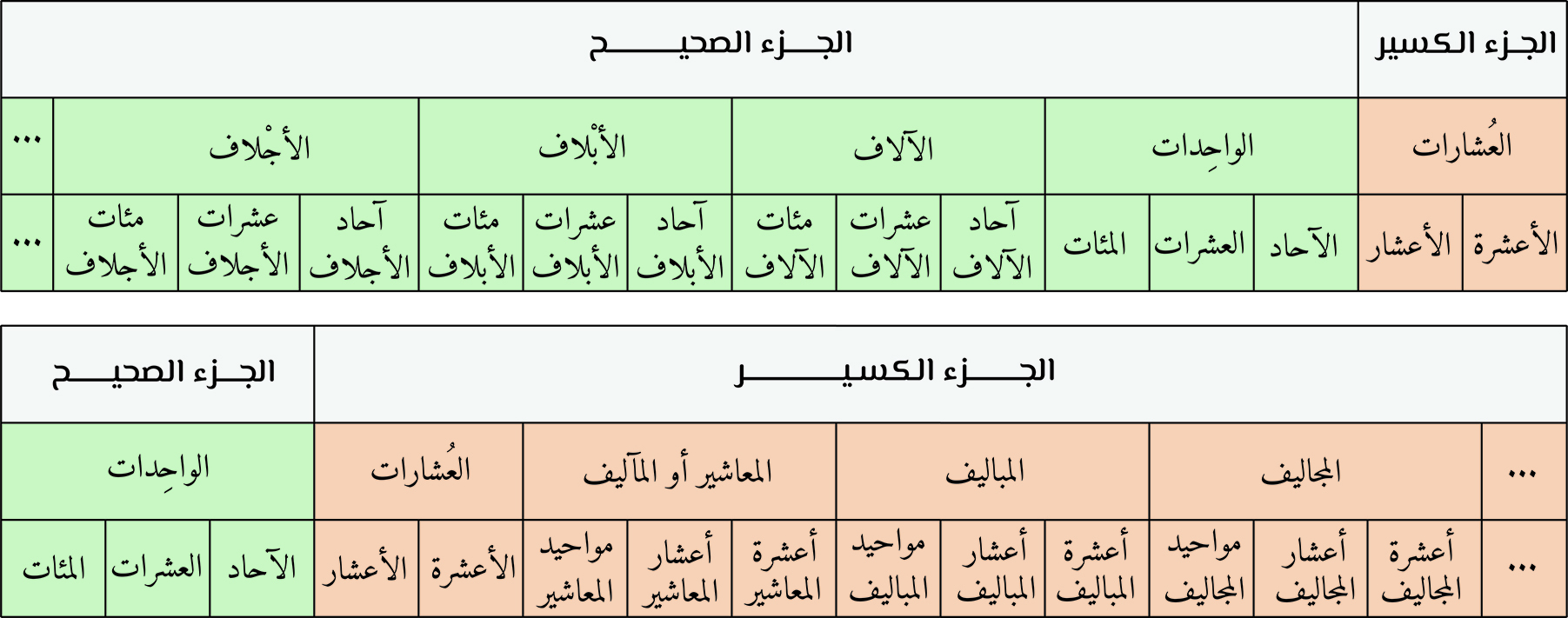
تكون قراءة الأعداد في العربية على نحو يمنع اللبس ويدفع الوقوع في الخطأ، وهذه أمثلة في قراءة بعض الأعداد الصحيحة والكسيرة أو العشرية في العربية:

89.000 = تسعة آلاف وثمانون، من دون تكرار كلمة ألف، فالأصل هو تسعة آلاف وثمانون ألفا، وحذفت الألْف الثانية لأنّ العشرات والمئات بعد الوِحدة من الوحدة، كما أنّ هذا العدد لا يُقرأ على شكل: تسعة وثمانون ألفا، لأنّه عدد آخر يُمثَّل له بالأرقام التالية: 80.009

65.874.236 = ستة وثلاثون ومئتان، وأربعة آلاف وسبعون وثمانمئة، وخمسة أبْلاف وستون.

695.321.458.746.254 = أربعة وخمسون ومئتان، وستة آلاف وأربعون وسبعمئة، وثمانية أبلاف وخمسون وأربعمئة، وجلف وعشرون وثلاثمئة، وخمسة أدلاف وتسعون وستمئة.

وتجري الأعداد المركّبة في القراءة مجرى الأعداد المفردة، ويقصد بها الأعداد من أحد عشر إلى تسعة عشر، لذلك لا يُفصل بين الآحاد والعشرات فيها باسم الصاتمة، وتكون قراءتها على هذا النحو:

11.000= أحد عشر ألفا. ولا يُقال: ألف وعشرة

12.000.000= اثنا عشر بَلْفا. ولا يُقال: بلفان وعشرة.

13.000.000.000= ثلاثة عشر جَلْفا. ولا يُقال: ثلاثة أجلاف وعشرة

14.000.000.000.000= أربعة عشر دَلْفا. ولا يُقال: أربعة أدلاف وعشرة.

15.000.000.000.000.000= خمسة عشر هَلْفا. ولا يُقال: خمسة أهلاف وعشرة.

ويُقرأ هذا العدد 211.456= ستة وخمسون وأربعمئة وأحد عشر ألفا ومئتان، أمّا إذا كان العدد غير مركّب، فيُقرأ بفصل الآحاد عن العشرات بالصاتمة، فيُقال على سبيل المثال في هذا العدد: 569.821= واحد وعشرون وثمانمئة وتسعة آلاف وستّون وخمسمئة. ولا يُقال واحد وعشرون وثمانمئة وتسعة وستّون ألفا وخمسمئة، كما لا يُقال أيضا: واحد وعشرون وثمانمئة وتسعة وستّون وخمسمئة ألف.

أمّا الأعداد الكسيرة أو العشرية فهناك طريقتان لقراءتها، الأولى: هو أن يُقرأ العدد الكسير قراءة العدد الصحيح مع إضافة اسم قيمة القُصارة (الخانة) الأخيرة جهة اليمين.

0,7 = سبعة أعشار.

0,45 = خمسة وأربعون عشيرا.

0,526 = ستة وعشرون وخمسمئة مِعْشار أو مِئْلاف.

0,5698214 = أربعة عشر ومئتان وثمانية آلاف وتسعون وستمئة وخمسة أبْلاف أعْشِرةِ مِبْلاف، أي أنّ هذا العدد 0,5698214 هو جزء من أعْشِرة مِبلاف.

أمّا الطريقة الثانية فهي الأضبط والأسهل، حيث تكون فيها قراءة الأعداد الكسيرة كقراءة الأعداد الصحيحة تماما. تتحقّق هذه الطريقة باعتماد أسماء جديدة للأعداد الكسيرة على نحو ما عليه الأعداد الصحيحة حيث تُشتق الأسماء الجديدة من أسماء الأعداد الصحيحة بالاشتقاق الكبير، وهو القلب المكاني للحروف، ولمّا كانت قراءة العدد العشري في اتجاه يُعاكس قراءة العدد الصحيح فإنّ القاعدة تنصّ على أن تكون أسماء الأعداد العشرية عكسا لأسماء الأعداد الصحيحة أيضا مع مراعاة السهولة في نطق اللفظ، فالعدد سَبْعة يُقابل الجزء عَبْسة وتِسْعة تُقابل الجزء عِسْتة وستّة تُقابل الجزء تِسَّة، وألف تقابل الجزء فَلْأ وجَلْف تقابل الجزء فَلْج، وبهذا نشتقّ أسماء جديدة من صميم العربية وفي الوقت نفسه تكون سهلة في الحفظ والادراك، فالآحاد تُقابلها المواحيد، والأعشار تقابلها الأرشاع، والمئات تقابلها الإمات، والآلاف تقابلها الأفْلاء، والأبْلاف تقابلها الأفْلاب، والأجْلاف تُقابلها الأفلاج، وهكذا دواليك إلى الأشلاف وتقابلها الأفلاش.

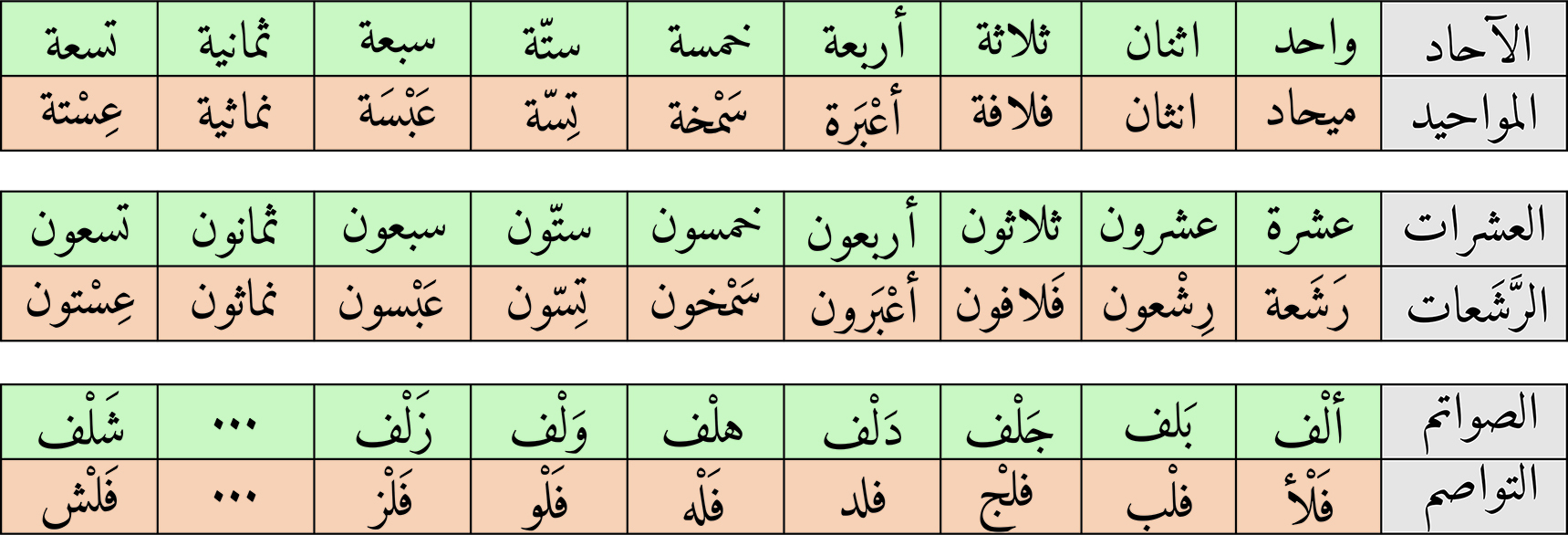
0,1= رَشَعة؛

0,2= رِشْعون؛

0,3= فلافون. إنّ القلب المكاني لحروف العدد ثلاثة يُعطي ثلاثة أيضا، واُختيرت الفاء لتعويض الثاء لأنّها قريبة لها في المخرج، ولأنّ الفاء حرف من حروف الذلاقة، ويصحّ فيها سلاسة أيضا، لأنّ السين والثاء لهما المخرج نفسه.

0,4= أعْبَرون؛

0,5= سَمْخون؛

0,6= تِسُّون؛

0,7= عَبْسون؛

0,8= نَماثون؛

0,61= تِسّون وإمة. الإمة هي قلب لمِئة، ويُقال فيها أيضا إمَتان من مِئتان، وفلافُئِمة من ثلاثمئة، وأعْبرُئِمة من أربعمئة، وسَمْخُئِمة من خمسمئة، وتِسُّئِمة من ستّمئة، وعَبْسُئِمة من سبعمئة، ونماثِئِمة من ثمانمئة، وعِسْتُئِمة من تسعمئة.

0,537= سمْخون وفلافئمة وعَبْسة أفْلاء؛

0,69.72= تِسّون وعِسْتُئِمة وعَبْسة أفْلاء ورِشْعون؛

0,57.632.367.415= سمخون وعَبْسُئِمة، وتِسّة أفْلاء وفلافون وإمَتان، وفلافة أفْلاب وتِسّون وعبسئمة، وأعْبَرُ أفْلاج ورَشَعة وسَمْخُئِمة.

1,5= واحد وسمخون؛

3,8= ثلاثة ونماثون؛

10,9= عَشَرة وعِسْتُون؛

26.954.317,98.314.57= سبعة عشر وثلاثمئة، وأربعة آلاف وخمسون وتسعمئة، وستّة أبْلاف وعشرون. وعِسْتون ونماثئِمة، وفلافة رَشَعَ أفلاء وأعبرئمة وسمخة أفلاب وعَبْسون. وتأخذ هذه الأسماء المصطنعة بالاشتقاق الكبير أحكامها من أحكام العدد في العربية، من حيث الإضافة والتأنيث أو التذكير والعدد والمعدود، الخ.

المِيحاد في الأصل غير موجود، لأنّ العدد الكسير يبدأ بالأعشار، لذلك يقال الأعداد العشرية، فالعدد الذي يكون على يسار الصفر أو أعلى من الصفر، فهو من العشرات، أمّا العدد الذي يكون على يمين الصفر أو أدنى من الصفر، فهو من الأعشار.